Metody i algorytmy planowania ruchu - laboratorium

Lab 6 - Algorytmy poszukiwania ścieżki próbkujące przestrzeń poszukiwań na przykładzie RRT (Rapidly-exploring Random Tree)

1. Wprowadzenie

Celem zajęć jest zapoznanie się z jednym z podstawowych algorytmów poszukiwania ścieżki łączącej 2 punkty, który wykorzystuje losowe próbkowanie przestrzeni poszukiwań.

Tym razem nie będziemy przeszukiwać już danego grafu, lecz tworzyć własny graf przeszukiwań, który nie będzie aż tak ograniczony jak grafy-siatki wykorzystywane na poprzednich zajęciach.

Tego typu metody są szczególnie przydatne, gdy przestrzeń poszukiwań jest bardzo duża, gdyż nie wymagają one operacji na bardzo dużych grafach.

⚠️ Pamiętaj, aby w każdym nowym terminalu zanim rozpoczniesz pracę skonfigurować środowisko ROS komendą
source /opt/ros/humble/setup.bash lub source install/setup.bash

2. Przygotowanie paczki w ROS

Zainstaluj paczkę ros-humble-nav2-map-server:

sudo apt-get install ros-humble-nav2-map-server ros-humble-nav2-lifecycle-manager

Pobierz paczkę z zadaniami z repozytorium github:

cd ~/ros2_ws/src
git clone  https://github.com/BartlomiejKulecki/mapr_6_student.git

Następnie skompiluj pobraną paczkę i odśwież przestrzeń roboczą:

cd ~/ros2_ws
colcon build --symlink-install
source install/setup.bash

Pliki points.py oraz grid_map.py są podobne do tych, które mieliście do dyspozycji na poprzednich zajęciach, aczkolwiek zostały one dopasowane do nowej sytuacji, gdy mapa będzie nam służyła jedynie do sprawdzania poprawności ścieżek, a nie będzie przestrzenią poszukiwania jako taką (nie będzie stanowić grafu poszukiwań).

3. Uproszczony algorytm RRT

Uproszczony algorytm RRT należy zaimplementować w pliku rrt_vertices.py

Aby ułatwić wam zadanie, zaczniemy od implementacji funkcji które użyte razem, w odpowiedni sposób złożą się na uproszczony algorytm RRT. Jednakże, jeśli uważasz, że jesteś w stanie poradzić sobie bez tych ułatwień, po prostu od razu zaimplementuj algorytm opisany w zadaniu 3.5.

Aby ułatwić wyświetlanie drzewa przeszukiwań, została zaimplementowana metoda publish_search, która publikuje wizualizację drzewa przeszukiwań, przy czym zakłada ona, że drzewo to jest reprezentowane poprzez słownik self.parent, który zawiera krawędzie drzewa zdefiniowane jako para klucz, wartość, gdzie klucz jest wierzchołkiem dzieckiem, a wartość jego wierzchołkiem rodzicem.

Implementację niektórych funkcjonalności może wam ułatwić biblioteka numpy i funkcje takie jak:

• np.linalg.norm
• np.random.random
• np.random.seed
• np.linspace

oraz inne działania na wektorach liczb. Pod adresem https://pkicki.github.io/ możecie znaleźć krótkie wprowadzenie do tej biblioteki wraz z przykładami.

🔨 Zadania:

3.1 random_point()

Napisz metodę, która zwraca losowy punkt w dwuwymiarowej przestrzeni zadania T = [0; self.width] ⨉ [0; self.height].

3.2 find_closest(point)

Napisz metodę, która zwraca najbliższy punktowi point wierzchołek drzewa przeszukiwania.

3.3 new_point(random_point, closest_point)

Napisz metodę, która zwróci punkt należący do odcinka łączącego closest_point i random_point znajdujący się w odległości self.step od closest_point.

3.4 check_if_valid(point_1, point_2)

Napisz metodę, która sprawdzi czy odcinek łączący point_1 i point_2 nie wychodzi poza przestrzeń zadania T oraz czy nie jest w kolizji z przeszkodą zaznaczoną na mapie self.map. Możesz to zrobić w sposób przybliżony, wybierając np. 100 równoodległych od siebie punktów na tym odcinku i sprawdzając czy każdy z nich leży w przestrzeni wolnej.

3.5 search()

Napisz metodę, która realizuje następujący pseudokod:

1. Zainicjalizuj drzewo przeszukiwań początkowym wierzchołkiem self.start
2. Wylosuj punkt na mapie
3. Znajdź najbliższy mu wierzchołek należący do drzewa przeszukiwań
4. Utwórz nowy punkt, który leży na odcinku łączącym punkty wyznaczone w podpunktach 2 i 3 w odległości self.step od punktu z podpunktu 3.
5. Sprawdź, czy odcinek łączący nowy punkt z najbliższym mu wierzchołkiem w grafie leży w przestrzeni wolnej.
6. Jeśli tak, to dodaj ten nowy punkt do drzewa przeszukiwań.
7. Wyświetl drzewo przeszukiwań poleceniem self.publish_search()
8. Sprawdź, czy z nowego punktu da się bezkolizyjnie połączyć z punktem końcowym self.end.
9. Jeśli tak, to dodaj go do drzewa, wyświetl rozwiązanie (metoda self.publish_path(path)) i zakończ algorytm.
10. Jeśli nie, wróć do punktu 2.

Kod uruchamia się poleceniem:

ros2 launch mapr_6_student rrt_launch.py vertices:=True

Spodziewany efekt dla np.random.seed(44) i self.step = 0.05:

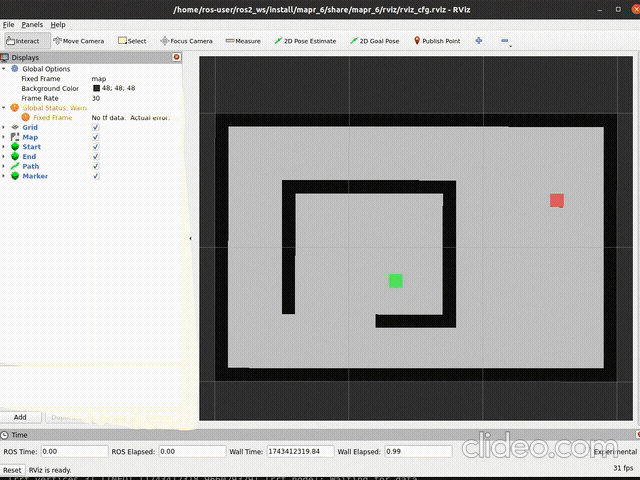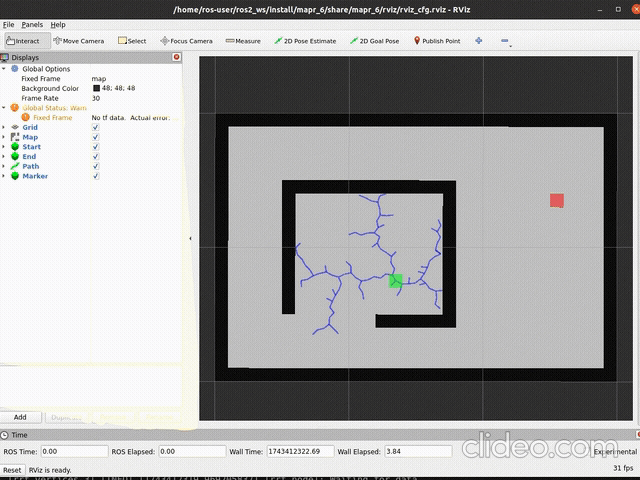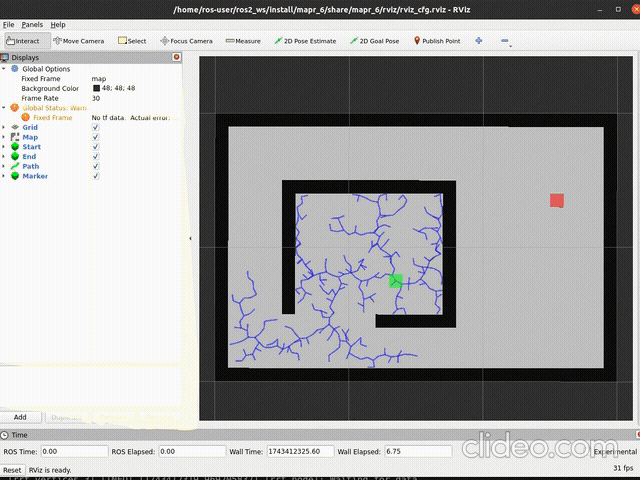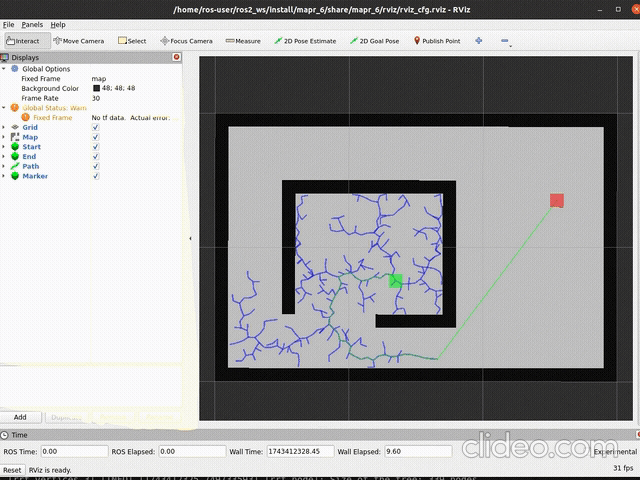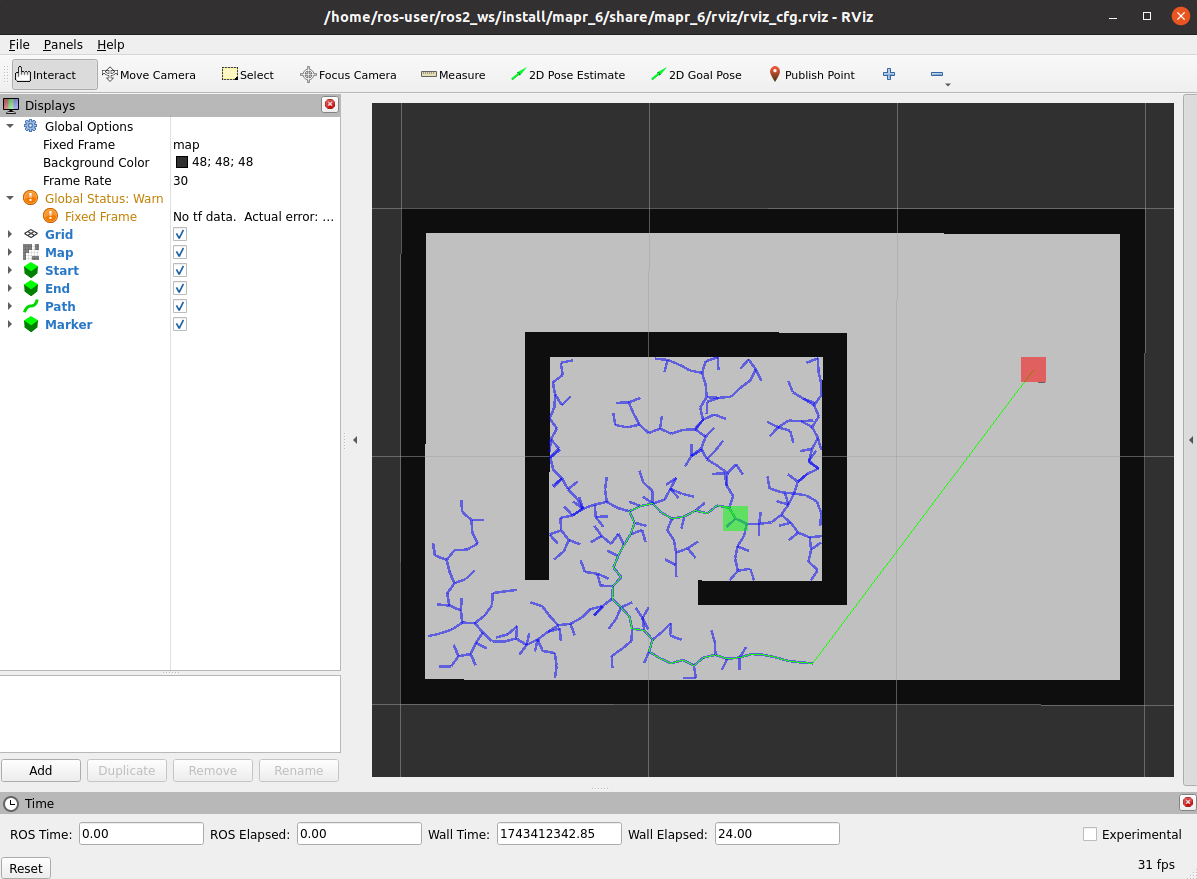działanie	stan końcowy

Spodziewany efekt dla np.random.seed(44) i self.step = 0.1:

4. Algorytm RRT (zadanie dla chętnych 💪)

Algorytm RRT należy zaimplementować w pliku rrt.py

Kod uruchamia się poleceniem:

ros2 launch mapr_6_student rrt_launch.py

🔨 Zadania:

4.1 find_closest(point)

Zmodyfikuj metodę tak, aby zwracała ona najbliższy punktowi point punkt na grafie, tj. najbliższy wierzchołek, bądź najbliższy punkt na krawędzi. Jeżeli jest to najbliższy punkt na krawędzi, to rozdziel tę krawędź na dwie - łączącą punkt bliższy korzeniowi i wyznaczony punkt na krawędzi, oraz ten punkt i punkt dalszy korzeniowi (konieczne jest to dla zachowania spójności grafu).

4.2 new_point(random_point, closest_point)

Zmodyfikuj metodę tak, aby zwracała ona ostatni (licząc od closest_point do random_point) punkt należący do odcinka łączącego closest_point i random_point (zakładamy podział odcinka na 100 równoodległych punktów), który leży w przestrzeni wolnej (zob. obrazek).

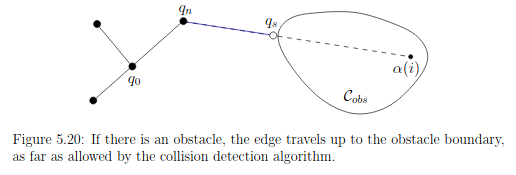
4.3 search()

Zmodyfikuj metodę, tak, aby realizowała algorytm opisany w punkcie 3. wykorzystując dostępne metody (w ich najnowszych wersjach).

Spodziewany efekt dla np.random.seed(444):

Warto również zakomentować część odpowiedzialną za zatrzymanie algorytmu i zobaczyć jak się będzie zachowywał w granicy dla liczby iteracji dążącej do nieskończoności np. 5000:

Oryginalny opis algorytmu RRT:

http://msl.cs.uiuc.edu/~lavalle/papers/Lav98c.pdf

http://planning.cs.uiuc.edu/booka4.pdf